Dynamic Programming Optimization - Convex Hull Trick

Convex Hull Trick (DP Optimization), সংক্ষেপে CHT নামটা হয়ত অনেকেই শুনে থাকবেন। সবার মনেই প্রথম প্রশ্ন জাগে “আমি তো Convex Hull ই পারি না, তাহলে CHT শিখব কি করে ”। আসলে Geometry এর Convex Hull আর Dynamic Programming এর Convex Hull Trick আসলে ২টা একেবারেই ভিন্ন জিনিস।

Prerequisites

• Coordinate Geometry এর প্রাথমিক ধারণা থাকা।
• Line Equation সম্পর্কে ধারণা থাকা (ক্লাস ৯-১০ পর্যন্ত ভাল করে থাকলেই হবে)।
• 2D Dynamic Programming এর বেশ কিছু Problem Solve করা।
• Binary / Ternary Search সম্পর্কে ধারণা থাকা।
• Graph আঁকানোর জন্য খাতা-কলম নিয়ে বসলে ভাল হয়।

What is this Convex Hull Trick?

আগে আমরা Dynamic Programming Optimization এর দিকে না যাই। আগে দেখি Convex Hull Trick জিনিসটা কি। এর পরে এইটা ব্যবহার করে কিভাবে Dynamic Programming Optimize করা যায় সেটা দেখব।

CHT আসলে একটা Data Structure এর মত, যেইটা কিছু Linear Function $f_i(x) = m_ix + b_i$ maintain করে। আর আমরা Query করতে পারি কোন একটা $x$ এর জন্য $max/min\left\lbrace f_i(x)\right\rbrace$ কত হতে পারে।
যেমনঃ CHT তে যদি এই function গুলা থাকে -

• $f_1(x) = 4x + 3$
• $f_2(x) = 3x - 2$
• $f_3(x) = -5x + 15$

তাহলে আমরা $4$ দিয়ে Query করে Maximum চেলে উত্তর পাব $max\lbrace f_1(4), f_2(4), f_3(4)\rbrace = max\lbrace 19, 10, -5\rbrace = 19$

Convex Hull Trick এর ২টা Version আছে -

• এক ধরনের CHT তে আমরা ইচ্ছা করলেই Random line add করতে পারি না, কিছু Condition মানতে হয়, যেমনঃ $m_1 \geq m_2 \geq \cdots \geq m_i \geq m_{i+1}$ অথবা $m_1 \leq m_2 \leq \cdots \leq m_i \leq m_{i+1}$ এইরকম। এটাকে আমরা Semi-offline CHT বলতে পারি।
  এইধরনের CHT তে আমরা $O(1)$ Amortized (অর্থাৎ $O(n)$ overall) Complexity তে নতুন Line add করতে পারি। আবার $O(\log n)$, অথবা বিশেষ শর্ত সাপেক্ষে $O(1)$ Amortized Complexity তে Query করতে পারি।
• আরেক ধরনের আছে যেইটাতে ইচ্ছা মত Random Line Add করা যায়। সেইটাকে Dynamic CHT বলে। এইধরনের CHT তে $O(\log n)$ এ নতুন Line add বা Query করা যায়।

এই Tutorial শুধুমাত্র Offline CHT এর মধ্যে সীমাবদ্ধ থাকবে।

Basic Idea

প্রথমে আমরা যা করব, Function গুলাকে Plot করে ফেলব।
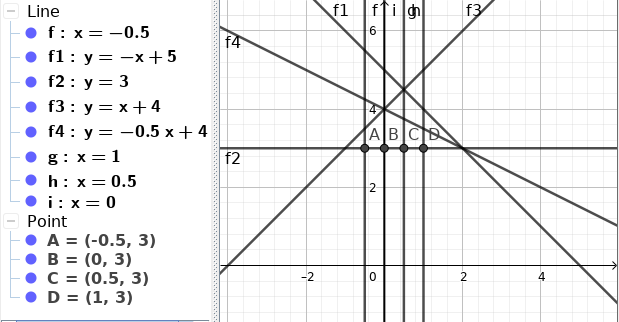
মনে করি, আমাদের Function গুলা হল -

Function গুলা Plot করে ফেলি -

মনে করি আমাদের Query Point হল $1$। তাহলে কোন একটা Function $f$ এর জন্য $f(1)$ হবে $x = 1$ Line টা $f$ function এর line কে যেই বিন্দুতে ছেদ করে তার $y$ এর value.

যেমন: উপরের function গুলার জন্য $x = 1$ line যেইসব বিন্দুতে ছেদ করে -

Plot থেকে দেখতে পাই যে, $f_1(1) = A_y = 4$, $f_2(1) = B_y = 3$, $f_3(1) = C_y = 5$ এবং $f_4(1) = 3.5$।
এখানে Minimum value হল $B_y = 3$, মানে সবচেয়ে নিচের দিকে যেই ছেদবিন্দু তা হয়েছে সেইটার $y$ এর value.

এখন একটা Observation করা যায় -
উপরের Function গুলার জন্য, CHT তে যদি আমরা Minimum maintain করতে চাই তাহলে আমাদের কি $f_4$ এর আদৌ কোন দরকার আছে? যেকোনো Point এর জন্য আমরা যদি Query করি, $f_4$ কি কখনো আমাদের Minimum Value দিতে পারবে?

যেমন, আরও কিছু Query Point $\lbrace -2, 0, 3\rbrace$ এর জন্য Line আঁকিয়ে দেখতে পারি -

এখানে $A, B, C$ Point গুলার কোনটাই $f_4$ এর Line এর উপরে নাই। লক্ষ্য করলে দেখব আমরা Query যাই করি না কেন, $f_4$ কখনই Minimum Value দেবেনা, যদি আমাদের $f_1, f_2, f_3$ থাকে।

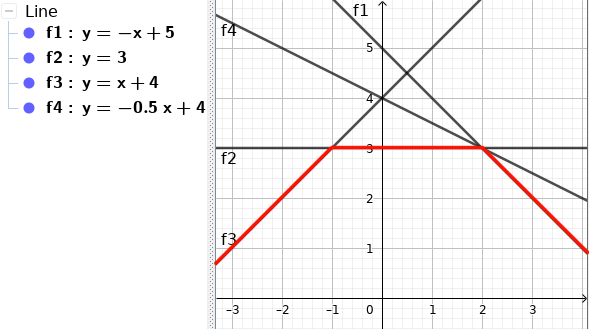
আরেকটা Observation আছে। একটা নির্দিষ্ট Range এর সব Query এর জন্য একটাই Function বার বার Minimum Value দেবে। যেমন -

এইখানে সব গুলা Query এর জন্য শুধু $f_2$ Minimum value দিচ্ছে। আসলে, যেকোনো $x \in [-1, 2]$ এর জন্যই $f_2$-ই Minimum দেবে।

এখন আমরা CHT এর Main Idea টা বলতে পারি, সেইটা হল প্রয়োজনীয় Line গুলা, মানে যে Line গুলা কখনো না কখনো Minimum value দিতে পারে সেইগুলা রেখে বাকি সব Line বাদ দিয়ে দেওয়া।

আরেকটা জিনিস আমরা লক্ষ্য করতে পারি, যেই Line গুলা আমরা CHT তে রাখতে চাচ্ছি, তাদের যেই অংশ গুলা কাজে লাগে সেইগুলা একটা Half Convex Hull গঠন করে। এদের Upper Hull/Lower Envelope এবং Lower Hull/Upper Envelope বলে। যেমন উপরের Function গুলার জন্য যদি আমরা Minimum maintain করতে চাই তাহলে শুধু এই অংশ গুলা কাজে লাগে -

এরা একটা Convex Hull এর উপরের অংশও তৈরি করেছে। তাই একে Upper Hull বলা যায়।
আমরা যেকোনো Query-ই করি না কেন, Minimum value এই অংশগুলা মানে এই Lower Envelope এর উপরেই থাকবে।
আবার একই ভাবে আমরা যদি Maximum maintain করতে চাই তাহলে Lower Hull/Upper Envelope maintain করলেই হবে -

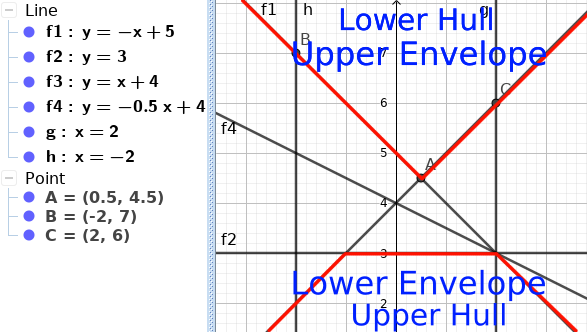
সুতরাং, Maximum Value গুলা সব Lower-Hull এর উপরে, আর Minimum Value গুলা সব Upper-Hull এর উপরেই থাকবে। এ জন্য আমরা যখন Minimum maintain করব তখন Upper-Hull এর অংশগুলা রেখে বাকি সব Line বাদ দেব। আবার যখন Maximum maintain করব, Lower-Hull এর অংশগুলা রেখে বাকি Line গুলা বাদ দেব। এইটাই CHT এর মূল বিষয়।

Being more formal

এই পর্যন্ত যা যা লিখলাম সেইটা বুঝে থাকলে সামনে যেতে পারেন।
এখনো পর্যন্ত আমরা যেইটা জানি না সেইটা হল, একটা Line যে আমাদের লাগবে না তা বুঝব কি করে?
আমরা ধরে নেই যে আমাদের যেই Line গুলা দেওয়া আছে সেইগুলার জন্য

মনে করি, আমরা $i^{th}$ line add করছি এখন। আর আমাদের $i - 1$ টা Line আগেই Add করা হয়ে গেছে। তাহলে আমাদের Line গুলা একটা Lower Hull বানিয়ে ফেলছে নিশ্চয়ই। ধরি এইরকম -

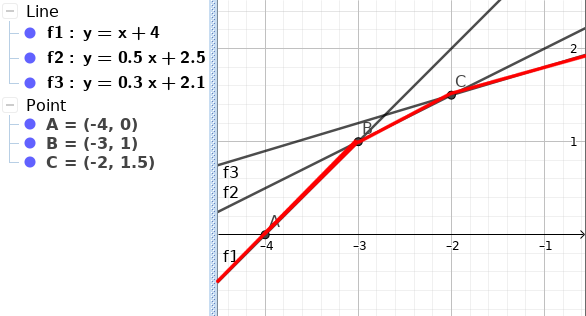
এখন লক্ষ্য করি, এর পরের বার আমরা যেই Line টা add করব সেইটা কিন্তু কখনই এইরকম হবে না -

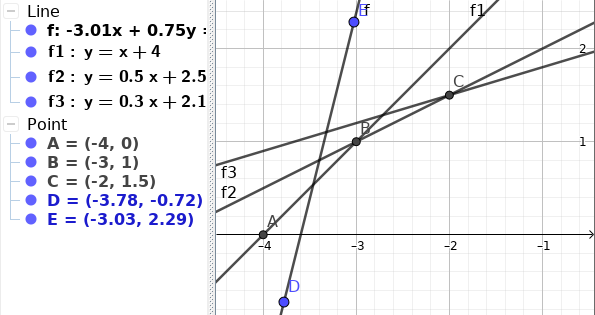
কারণ কি? এর কারণ হল আমরা ধরে নিয়েছি যে $m_{i-1} > m_{i}$। কিন্তু এই Line এর Slope আসলে বেশি হয়ে গিয়েছে। এজন্য দেখা যায় যে, আমরা মাত্র ২ ধরনের Line পেতে পারি -

প্রথমত, এক রকম Line আসতে পারে যেইটা আসার পরে শুধু মাত্র শেষের Line এর একটা অংশ থেকে পরের সব নিজের করে ফেলবে, মানে শেষ Line এর একটা অংশের পরের সব Query এর জন্য ওই Line ই Minimum দিবে। যেমন, এইরকম Line আসতে পারে -

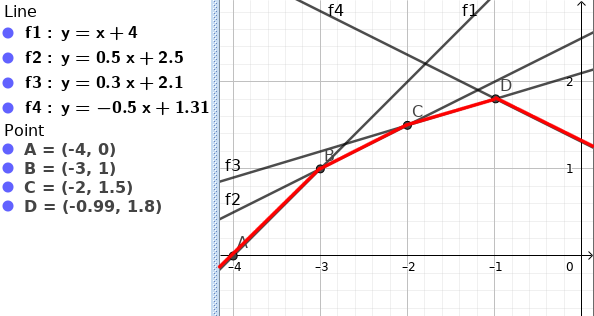
আগে $D$ Point এর পরের সব Query এর জন্যও $f_3$ Minimum দিত। কিন্তু এখন $D$ এর পরের সব Point এর জন্য $f_4$ Minimum দিবে। এইরকম হলে কি করতে হবে সেইটা পরিষ্কার, আমরা এইটাকে CHT তে নিয়ে নিলেই হল।

দ্বিতীয়ত, আরেক ধরনের Line হতে পারে, যেইটা আগের অনেক Line এর Range এর মধ্যেও Minimum দিতে পারে। যেমন -

এখানে একটা জিনিস খেয়াল করি, যেইসব জায়গায় $f_3$ Line minimum দিচ্ছিল এখন সেইসব জায়গায় $f_4$ Line minimum দিচ্ছে -

এইখানে অবশ্যই $C$ থেকে $G$ ভাল, আবার $F$ থেকে $E$ ভাল। আসলে এখন $f_3$ এর আর দরকারই নাই। আবার, আগে $BC$ এর মধ্যে সব Query পড়ত $f_2$ এর উপরে, কিন্তু এখন $DC$ অংশের সব Query পড়বে $f_4$ এর $DG$ এর উপরে। তাই $f_3$ এর মোটেও দরকার না থাকলেও $f_2$ এর দরকার আছে। তাই $f_3$ বাদে এখন আমাদের নতুন Hull হবে -

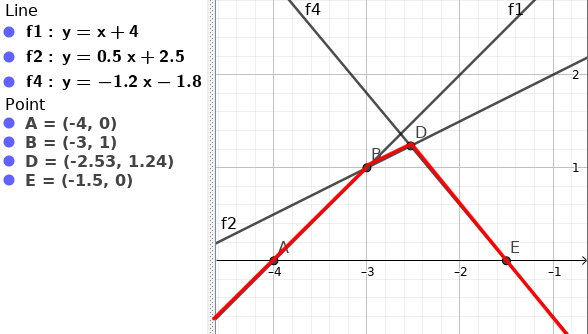
আবার আমাদের নতুন Line যদি এইরকম হত -

তাহলে কিন্তু $f_2$ আর $f_3$ ২টা Line এর-ই আর কোন দরকার থাকত না। তখন নতুন Hull হতো এইরকম -

তাহলে আমাদের কি করতে হবে এখন পরিষ্কার, আমাদের আগের ২টা Line দেখে বলতে হবে যে আমাদের নতুন Line টা Hull এ থাকবে নাকি থাকবে না। আবার থাকলেও, আগের Line টা কে রাখবও নাকি রাখবও না।

এখন আমরা শুধু ৩টা Line নিয়ে চিন্তা করি, মনে করি এমন -

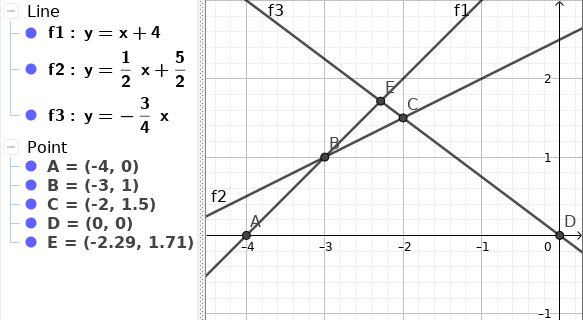
এইখানে আমাদের $f_2$ আর $f_3$ উভয়কেই রাখতে হবে। কারণ $f_2$ এর $BC$ অংশের প্রয়োজনীয়তা আছে।

আবার এইরকম হতে পারে -

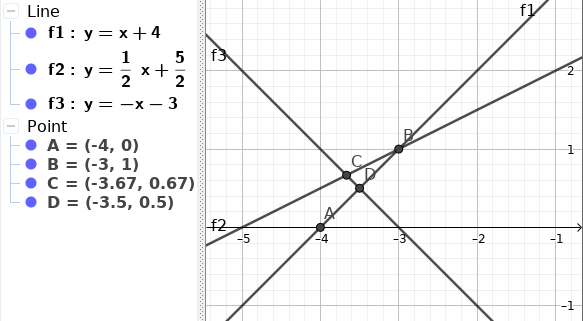
এক্ষেত্রে আর $f_2$ এর দরকার নাই।

উপরের ২টার ক্ষেত্রেই, বা আমরা আরও আঁকিয়ে দেখতে পারি যে আসলে, $f_1$ এর সাথে $f_3$ এর intersection point (উপরের Plot এ Point $D$) যদি $f_1$ এর সাথে $f_2$ এর intersection point (উপরের Plot এ Point $C$) এর বামে হয় তাহলে আমাদের $f_2$ এর আর কোন দরকার নাই। আর ডানে হলে আমরা $f_3, f_2$ ২টাকেই রেখে দিতে পারি।
এইটা কাজ করবে যখন আমাদের Line গুলার $m_1 \geq m_2 \geq \cdots \geq m_{i-1} \geq m_i$ হবে, আর আমরা Minimum maintain করতে চাই।

আসলে আমরা ৪ ধররেন Offline CHT পেতে পারি -

• $m_1 \geq m_2 \geq \cdots \geq m_{i-1} \geq m_i$, Minimum Query
• $m_1 \geq m_2 \geq \cdots \geq m_{i-1} \geq m_i$, Maximum Query
• $m_1 \leq m_2 \leq \cdots \leq m_{i-1} \leq m_i$, Maximum Query
• $m_1 \leq m_2 \leq \cdots \leq m_{i-1} \leq m_i$, Minimum Query

এই ৪ ধরনের জন্যই আমরা একই ভাবে ৩টা Line আঁকিয়েই বের করতে পারি যে $f_1, f_2, f_3$ এর মধ্যে $f_2$ কে আমরা কোন শর্তে বাদ দেব। সেটা "Left as an exercise to the readers".

Implementation

এখন এইটা Implement করা যাক। এখানে খালি $m_i \geq m_{i+1}$ আর Minimum maintain করে এমন CHT Implement করব। বাকিগুলাও খালি একটা condition পরিবর্তন করেই বানানো যাবে।

শুরুতেই আমরা Line-গুলার Slope আর Constant store করার জন্য ২টা array/vector নিয়ে নিতে পারি -

vector<long long> m, b;

এখন আমাদের একটা Helper Function লাগবে, যেইটা বলবে $f_1, f_2, f_3$ এর মধ্যে $f_2$ কে আমরা বাদ দেবও নাকি। উপরের অলোচনা থেকে আমরা জানি যে, ${(f_1 \cap f_3)}_x < {(f1 \cap f2)}_x$ হলে আমরা $f_2$ কে বাদ দেব।
আবার ২টা Line, $y = m_1x + b_1, y = m_2x + b_2$ এর intersection point $(x, y)$ হল আসলে তাদের সমাধান $(x, y)$।
তাহলে সমাধান করা যাক -

এখন আমরা সহজেই function টা লিখতে পারি -

bool bad(int f1, int f2, int f3) {
  return double(b[f3] - b[f1]) / double(m[f1] - m[f3]) <=
         double(b[f2] - b[f1]) / double(m[f1] - m[f2]);  
}

কিন্তু এই function এ একটা সমস্যা আছে। double এ ভাগ করে Compare করতে গেলে Precision error হতে পারে। এজন্য আমরা একটা কাজ করতে পারি - Inequality টা আড়গুণ করে ফেলতে পারি। তাহলে function টা হবে -

bool bad(int f1, int f2, int f3) {
  return (b[f3] - b[f1]) * (m[f1] - m[f2]) <=
         (b[f2] - b[f1]) * (m[f1] - m[f3]);  
}

এখন আর Precision error হওয়ার সম্ভাবনা নাই। কিন্তু এখন আরেকটা সমস্যা আছে, সেইটা হল Overflow হতে পারে। কারণ b, m ২টাই সর্বচ্চ $10^{18}$ হতে পারে। তাই তাদের গুণফল $10^{36}$ হতে পারে। এই জন্য একটা Work around আছে -

bool bad(int f1, int f2, int f3) {
  return __int128(b[f3] - b[f1]) * (m[f1] - m[f2]) <=
         __int128(b[f2] - b[f1]) * (m[f1] - m[f3]);  // only for gnu g++
  // or compare by taking the answer in double :D
  // as double can *store* at most 10^300 (with precision error :p)
  return 1.0 * (b[f3] - b[f1]) * (m[f1] - m[f2]) <=
         1.0 * (b[f2] - b[f1]) * (m[f1] - m[f3]);  
}

এখন আমরা add(m, b) function লিখতে পারি। যেইটা একটা $f(x) = mx + b$ function add করবে CHT তে -

void add(long long m_, long long b_) {
  m.push_back(m_); b.push_back(b_); // push in CHT
  int sz = m.size();
  // notice that f1 from discussion is in position sz - 3
  // f2 is in sz - 2, new line is in sz - 1
  while(sz >= 3 && bad(sz - 3, sz - 2, sz - 1)) {
    m.erase(m.end() - 2); // remove f2's m
    b.erase(b.end() - 2); // remove f2's b
    sz--; // size is decreased by 1
  } // we remove f2's while we can
}

হয়ে গেল CHT বানানো । এখন বাকি Query করা।

Query

Query অনেক ভাবে করা যেতে পারে। Minimum Query করছি ধরে নিয়ে কয়েকটা Approach বলছি -

Approach 1

আমরা যখন Query করছি যে $x$ input দিলে কোন function সবচেয়ে ছোট মান দেয়, তখন আসলে আমরা কি করছি দেখা যাক। যেমন, নিচের CHT তে যদি আমরা $x = -1.5$ Query করি তাহলে এমন হয় -

আমরা তো আসলে Query করে $E_y$ চাচ্ছি তাই না? তাহলে এই বিন্দু কোন Line এর উপরে আছে জানলেই হবে। এর পরে ওই Line এর function কে Query এর $x$ এ Evaluate করলেই আমাদের উত্তর পেয়ে যাব।
Line টা বের করা সোজাও। আমরা যদি Hull এর Line Store করার পাশাপাশি Line গুলার Intersection Point Store করে রাখি তাহলে সহজেই এটা করা যাবে।

আমরা এইরকম Approach এ আসতে পারি -

• পাশাপাশি ২টা Line এর intersection point গুলার $x$ এর value আমরা note করে রাখব।
• এখন একটা Query $x$ আসলে আমাদের সবচেয়ে বড় একটা intersection point বের করতে হবে যেন $P_x \leq x$ হয় (যেমন, উপরের Plot এ Point $C$ হল $E$ এর just আগের Point)। এর পরে ওই intersection point এর পরের/আগের Line টা তে $x$ কে Evaluate করলেই আমাদের উত্তর পেয়ে যাব। এইখানে আমরা ওই রকম Point বের করার জন্য intersection point গুলার list এর উপরে Binary Search করতে পারি। তাহলে Complexity $O(\log n)$।

এইটা Implement করা একটু ঝামেলা। add() function টা একটু Complex হয়ে যায়। Line pop করার সময় intersection point ও pop করতে হবে। আবার নতুন Line এর জন্য নতুন intersection poitn টা Push করেত হবে।

Approach 2

একটা Critical Observation এর মাধ্যমে আমরা CHT এর আরেকটা বৈশিষ্ট্য বের করতে পারি। নিচের Plot টা লক্ষ্য করি -

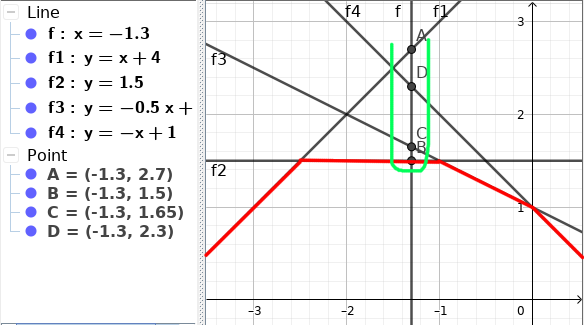
এখানে $x = -1.3$ এর জন্য এইটা $f_1, f_2, f_3, f_4$ কে যথাক্রমে $A, B, C, D$ Point এ ছেদ করেছে। আমাদের উত্তর হবে $B_y$ তাই না?
এখন লক্ষ্য করি যে, $A_y > B_y < C_y < D_y$
মানে আমাদের উত্তর যেইটা, সেইটা সবথেকে ছোট, কিন্তু এর আগে/পরে function এর value বাড়তে থাকে, বা intersection point এর $y$ এর value বাড়তে থাকো। আমরা আরও কিছু Plot করে দেখতে পারি, এইটা সব সময় সত্যি।

তাহলে আমরা আরেকটা Approach পেতে পারি এই Observation থেকে। যেহেতু আমাদের Answer যেই Line টা, সেইটার থেকে ২ দিকেই function এর value বাড়তে থাকে, তাই আমরা এই function এর index উপরে Ternary Search করতে পারি।
অনেকটা এইরকম -

ll f(int i, ll x) { return m[i] * x + b[i]; }
ll query(ll x) {
  int  lo = 0, hi = m.size() - 1;
  ll ans = -1e18;
  while(lo <= hi) {
    int mid1 = (lo + lo + hi) / 3;
    int mid2 = (lo + hi + hi) / 3;
    ll y1 = f(mid1, x), y1 = f(mid2, x);
    if(y1 <= y2) ans = y1, hi = mid2 - 1;
    else ans = y2, lo = mid1 + 1;
  } return ans;
}

একই রকম Observation আমরা বাকি ৩ ধরনের Offline CHT এর জন্যেও করতে পারি। এই Approach এর Complexity $O(\log_{1.5} n)$। এখানে আমরা integer ইনডেক্সের উপরে Ternary Search করছি; এই কাজটি আসলে Binary Search দিয়েও করা যায়। সেক্ষেত্রে আমাদের $f(i) \leq f(i + 1)$ এমন Variable এর উপরে Binary Search করতে হবে। এটি কাজ করে কারণ $f(i) \leq f(i + 1)$ একটি Prefix এ মিথ্যা আর বাকি Suffix এ সত্য। সেক্ষেত্রে Complexity $O(\log n)$।
Challenge: উপরের Ternary Search এর Code এ একটা Bug আছে, যার জন্য এইটা সব সময় সঠিক Answer দেয় না। বের করার চেষ্টা করেন।

Approach 3

আরেকভাবে Query করা যায়, যার জন্য আমাদের একটা Condition থাকতে হবে। সেইটা হল - $x_i \leq x_{i+1}$। মানে Query গুলা Non-Decreasing Order এ দেয়া থাকতে হবে।
আমরা Approach 1 থেকে দেখি যে আমরা আসলে পাশাপাশি ২টা Line এর Intersection point গুলার মধ্যে সবচেয়ে বড় যেইটা Query $x$ এর আগে আছে সেইটা বের করলেই Query Point কোন Line এর উপরে আছে সেইটা পেয়ে যাই। এখানেও আমরা একই রকম ভাবে করব, কিন্তু এখন আমাদের কাজ আরও সোজা।
যেমন, মনে করি আমরা কিছু Query Solve করেছই Already এইভাবে -

এখানে ২টা Query-ই $f_1$ Line এর উপরে পড়েছে। কিন্তু মনে করি আমরা এইরকম একটা Query পেলাম -

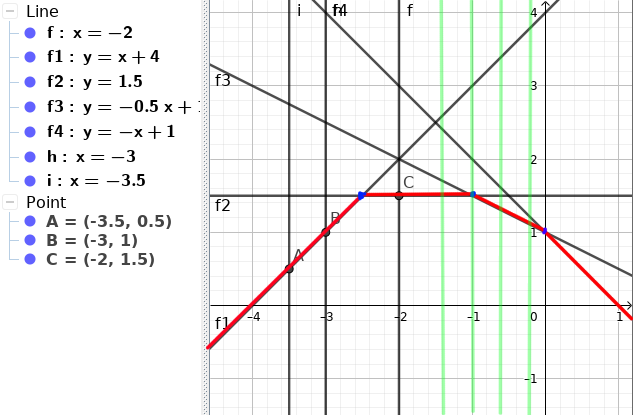
এখানে আমাদের Query $x_i = -2$, যেইটা $f_1, f_2$ এর Intersection পার করে গেছে। এখন আমরা লক্ষ্য করতে পারি যে, আমরা যেহেতু জানি সব Query এর জন্য $x_i \leq x_{i+1}$, তাহলে আমরা পরে আর যত Query-ই পাই না কেনও সেইটা $< x_i$ হবে না, হয় বড় নাহয় সমান হবে। তাই $x_i$ যে সব Intersection point পাড় করে গেছে সেইগুলার আগে যাবে এমন কোন Query পাওয়া সম্ভব না।

এই Observation থেকে আমরা আরেকটা Approach বের করতে পারি -

• আমরা একটা pointer রাখব যে এই পর্যন্ত আমরা কয়টা Intersection point পার করে ফেলেছি সেইটা note করবে।
• একটা নতুন Query আসলে আমরা জানি যে এইটা হয় বর্তমান Line এর উপরে, নাহলে এর পরের কোন Line এর উপরে থাকবে, কিন্তু কখনই আগের কোন Line এ থাকবে না।
• এখন আমরা দেখব, বর্তমান Line Query এর জন্য ভাল মান দেয়, নাকি এর পরের Line টা ভাল মান দেয়। পরের টা ভাল হলে pointer কে সেইটাতে নিয়ে যাব।
• যতক্ষণ আমরা পরের Line এ গেলে বর্তমান Query এর জন্য ভাল মান পাবও ততক্ষণ চলে যাব। কারণ আমরা জানি যে যেসব Line কে আমরা বাদ দিয়ে চলে যাচ্ছি তারা পরেও আর কোন কাজে আসবে না, যেহেতু Query non-decreasing.

এইটা Implement করা সবচেয়ে সোজা, অনেকটা এইরকম -

int ptr;
int query(ll x) {
  if(ptr >= m.size()) ptr = m.size() - 1;
  while(ptr < m.size() - 1 &&
    f(ptr, x) > f(ptr+1, x)) ptr++;
  return f(ptr, x);
}

এইখানে শুরুতে if(ptr >= m.size()) ptr = m.size() - 1 দেওয়ার কারণ হল যে, আমরা Hull এ নতুন Query করার সাথে সাথে Line add করার কারণে শেষের দিক থেকে কিছু Line বাদ হয়ে যেতে পারে। তখন আমরা শেষ Line টাতে ptr নিয়ে যাব।

এইটার Complexity amortized। কারণ এইখানে ptr একটা Query তে মাত্র ১ বার সরতে পারে, আবার একদম শেষেও চলে যেতে পারি। কিন্তু আমরা জানি যে আমাদের Line $O(n)$ টা আছে। তাই আমাদের ptr ও সমস্ত Query মিলিয়ে $O(n)$ এর বেশি সরতে পারবে না। এই জন্য এইটা $O(1)$ Amortized Complexity।

এখানে উল্লেখ্য যে এই Approach 3 কিন্তু উপরে বলা ৪টা Variation এর সব গুলাতে কাজ করবে না। যেইগুলাতে Line এর Index আগে থাকলে তার Intersection Point ও আগে থাকবে, শুধু সেইখানে এইটা কাজ করবে। অর্থাৎ, উপরে বলা Variation 1(Slope decreasing, minimum query) এবং 3(Slope increasing, maximum query) তে কাজ করবে এই Approach। কিন্তু বাকি গুলাতে যেইখানে Line এর Index সবার আগে, তার সাথে Intersection টা সবার পরে হয় ($x$ axis অনুযায়ী), তাই ওগুলাতে এইটা ব্যবহার করা যাবে না।

তবে হ্যাঁ, এই Approach আমরা ওইগুলাতে, মানে Variation 2, 4 এ ব্যবহার করতে পারব, যদি Query Decreasing হয়, মানে $x_i \geq x_{i+1}$ হয় Query তে। কারণ সামনের দিকের Line গুলা বড় $x$ এর জন্য Optimal value দেবে।

এই Approach কোথায় কোথায় ব্যবহার করা যাবে সংক্ষেপে মনে রাখার জন্য -

1. Slope decreasing, query minimum - তাহলে Query point গুলা হতে হবে increasing.
2. Slope increasing, query maximum - তাহলে Query point গুলা হতে হবে increasing.
3. Slope decreasing, query maximum - তাহলে Query point গুলা হতে হবে decreasing.
4. Slope increasing, query minimum - তাহলে Query point গুলা হতে হবে decreasing.

Implementation Practice

Direct CHT Implement করে এখানে Submit করে দেখতে পারেন - CHTPRAC - CHT Practice. একই সাথে ৪টা Variation ই Test করে দেখতে পারবেন।
Implement করতে সমস্যা হলে নিচে Comment এ জানাতে পারেন। (FB Account থাকলেই Comment করা যাবে)।

CHT এর পর্ব এইখানেই শেষ। এখন দেখা যাক এটা ব্যবহার করে কি করে Dynamic Programing Optimize করা যায়।

Dynamic Programming Optimization and Convex Hull Trick

একটা উদাহরণ দিয়ে বুঝানো যায় Dynamic Programming এ এইটা কিভাবে। শুরুতে একটা সোজা প্রবলেম নিয়ে বলি, যেইটা আসলে ঠিক DP না.

Problem Link: Bear and Bowling 4
এখানে বলা হয়েছে একটা Sequence $s_1, s_2, \cdots, s_k$ এর Score হল $\sum_{i=1}^k is_i$ এখন আরেকটা Array $a$ দেওয়া আছে। আমরা ইচ্ছা করলে $a$ এর কোন Suffix এবং / বা Prefix বাদ দিয়ে দিতে পারি। আমাদের Resulting sequence এর Score maximize করতে হবে।

শুরুতেই যেই Solution মাথায় আসে সেইটা হল Bruteforce। মনে করি, আমরা a[0..j] Prefix আর a[i+1 .. n] Suffix টা বাদ দেব। তাহলে বাকি থাকবে a[j+1 .. i]। আমরা i, j এর উপরে Bruteforce করে Maximum score নিতে পারি -

ll Max = 0;
for(int i = 1; i <= n; i++) {
  for(int j = 0; j < i; j++) {
    Max = max(Max, score(j, i));
  }
}

আমরা যদি score(l, r) বা a[l+1 .. r] এর Score যদি Naive ভাবে বের করি তাহলে এইটা হবে $O(n^3)$। এখন আমরা score(l, r) function এর জন্য কোন $O(1)$ formula বের করার চেষ্টা করতে পারি।

এখন এই Sum এর মধ্যে কিছু মৌলিক Sum এসেছে।
মনে করি -

বা সংক্ষেপে বললে p[i] = prefix sum of a[i], s[i] = prefix sum of i * a[i]। তাহলে আমাদের score(l, r) funtion টা আরও সহজে লেখা যায় -

এখন তাহলে আমরা আমাদের $O(n^3)$ Solution তা কে $O(n^2)$ করে ফেলতে পারি -

for(int i = 1; i <= n; i++) {
  for(int j = 0; j < i; j++) {
    Max = max(Max, s[i] - s[j] - j * p[i] + j * p[j]);
  }
}

এখন এইখানে আমরা আসলে কি করছি? প্রত্যেকটা Index $i$ এর জন্য আমরা আসলে এইটা করছি -

তাহলে এইটা কি দাঁড়াল? এইটা Exact CHT না?

তাহলে এখন আমাদের কি করতে হবে পরিষ্কার। আমাদের একটা CHT লাগবে, যেইটাতে আমরা একটা Index $i$ Process করার সময় সব $j < i$ এর জন্য $f_j$ function add করে রাখবো। যেখানে $f_j(x) = -j\cdot x + j\cdot p_j - s_j$।

তখন আমাদের আগের Bruteforce Code এর মধ্যে ভিতরে যেই Loop টা ঘুরছিল সেইটা আর লাগবেনা। সেইটা আমরা CHT তে $p_i$ দিয়ে Query করে তার সাথে $s_i$ যোগ করলেই পেয়ে যাব। কেননা, CHT তে আমাদের Line গুলা আছে হল - $\lbrace -j \cdot x + j\cdot p_j - s_j\rbrace$, এখানে $x$ এর জায়গায় $p_i$ বসিয়ে শেষে $s_i$ যোগ করলে আসলে score(j, i)-ই পাওয়া যায়।

তাহলে এখন Code করা যেতে পারে -

add(0, 0) // as we assume a[0] = 0
for(int i = 1; i <= n; i++) {
  Max = max(Max, query(p[i]) + s[i]);
  add(-i, i * p[i] - s[i]); // add line with m = -i and
                            // and b = i * p[i] - s[i]
                            // for later use
}

এইটা নাহয় main() function এর কাজ গেল। এখন আমাদের CHT এর ৪টা Varient এর কোনটা ব্যবহার করতে হবে সেইটা দেখা যাক।

আমরা Line add করছি যেইগুলা, তাদের $m$ হল যথাক্রমে -

$m_1 = -1, m_2 = -2, \cdots, m_i = -i$

মানে Slope গুলা decreasing order এ আছে। এবার দেখা যাক আমরা Query করছি আমরা কোন Order এ -

আমাদের মূল Array এর Number গুলা যেহেতু negative হতে পারে, তাই $x_i$ গুলা আসলে কোন Order maintain করে না।

তাহলে আমাদের একটা CHT Implement করতে হবে যেইটা Decreasing Slope এর Line add করতে পারে, Maximum maintain করে (Upper-Hull), আর Query যেহেতু কোন Order এ নাই, তাই Binary / Ternary Search করে উত্তর দেয়।

Complexity হল add() এর complexity আর query() এর complexity এর যোগফল। add() হল $O(1)$ amortized, আর Query হল $O(\log_2 n)$ বা $O(\log_3 n)$, Binary Search বা Ternary Search এর মধ্যে কোনটা ব্যবহার করা হয়েছে তার উপরে নির্ভর করে। তাহলে মোট Complexity $O(n \log n)$.

Another Problem:

NKLEAVES - Leaves: এখানে একটা Array দেওয়া আছে a[N]। সেটাকে $K$ টা Part এ ভাগ করতে হবে। প্রত্যেকটা Part এর Cost এর Sum Minimize করতে হবে।

একটা Part যদি হয় a[l..r] তাহলে এর Cost হল সবগুলা নাম্বারকে a[l] এ জমা করার Cost। একটা নাম্বার $a_i$ কে $x$ ঘর সরাতে Cost $x \cdot a_i$।

তাহলে আমরা একটা Cost Function বের করতে পারি। cost(l, r) = cost of a[l+1 .. r]। এই প্রবলেম এর Cost function প্রায় আগের প্রবলেম টার মতই। খালি $\lbrace 1\cdot a_1+ 2\cdot a_2+ \cdots +i\cdot a_i\rbrace$ এর বদলে $0 \cdot a_1 + 1\cdot a_2 + \cdots + (i-1)\cdot a_i \rbrace$।

আগের প্রবলেম এর মত আমরা এই Cost Function কে simplify করলে পাব -

এখন আমরা একটা DP State Define করতে পারি - $dp_k(i) = $ a[1..i] কে $k$ টা Part এ ভাগ করার Minimum Cost কত। [এখানে $k$ আর $K$ একই নয়]

Transition ও সোজা। আমরা সব Index $j < i$ এর উপরে Iterate করব। তাহলে a[1..i] কে $k$ টা Part এ ভাগ করার Cost হবে a[1..j] কে $k-1$ টা Part এ ভাগ করার Cost আর a[j+1..i] এর Cost এর যোগফল।

তাহলে একটা Code করা যাক, অনেকটা এইরকম -

// add base cases
for(int k = 2; k <= K; k++) {
  for(int i = 1; i <= N; i++) {
    for(int j = 1; j < i; j++) {
      dp[k][i] = min(dp[k][i], dp[k-1][j] + Cost(j, i));
    }
  }
}

এইটার Complexity $O(N^2K)$। এখন আমরা লক্ষ্য করলে সবচেয়ে ভিতরের Loop এর মধ্যে কিন্তু CHT দেখতে পাই । আমাদের ভিতরের পুরা Loop টাকে এখন Simplify করা যাক -

এখানে, $f_j(x) = -(j + 1) \cdot x + dp_{k-1}(j) - s_j + (j + 1) \cdot p_j$
বুঝতে সমস্যা হলে জানান।

মনে করি, আমাদের সব $dp_{k-1}(i)$ Calculate করা হয়ে গিয়েছে। তাহলে এখন এইগুলা Constant। তাই আমরা ঠিক আগের প্রবলেম এর মত করে এই প্রব্লেমেরও ভিতরের Loop টা কে বাদ দিয়ে দিতে পারি।

তাহলে এক কথায় বললে, আমাদের Bruteforce DP এর ভিতরের Loop এর জায়গায় আমরা শুধু CHT তে Query করব $p_i$ দিয়ে, এর পরে $s_i$ যোগ করলেই পুরা Loop এর কাজ হয়ে যাবে। আর সাথে সাথে আমাদের একটা Index $i$ process করার সময় সব Index $j < i$ এর জন্য $f_j$ add করতে হবে CHT তে। যেখানে $f_j(x) = -(j + 1) \cdot x + dp_{k-1}(j) - s_j + (j + 1)\cdot p_j$।

Code অনেকটা এইরকম হতে পারে -

// calculate base case dp[1][..]
for(int k = 2; k <= K; k++) {
  m.clear(), b.clear(), ptr = 0;
  add(0, 0); // This is for a[0] = 0, we assume
  for(int i = 1; i <= N; i++) {    
    dp[k][i] = query(p[i]) + s[i];
    add(-(i + 1), dp[k-1][i] - s[i] + (i + 1) * p[i]);
        // add for later use
  }
}

এইখানে আমরা যেসব Line add করছি সেইগুলার Slope গুলা -

মানে Slope decreasing আগের প্রবলেম এ আমাদের মূল Array তে Negative Number থাকতে পারত, কিন্তু এই প্রবলেম তা সব নাম্বার Positive। এজন্য যেকোনো $p_i \leq p_{i+1}$। আর আমরা যেহেতু $p_i$ দিয়ে Query করছি তাই Query গুলা Increasing Order এ আছে। এক্ষেত্রে আমরা উপরে দেখানো Approach 3 এর মত করে Query করে $O(1)$ Amortized Complexity পেতে পারি।

তাহলে মোট Complexity $O(NK)$

Problem Solving

CHT এর অনেক প্রবলেম পাওয়া যাবে বিভিন্ন Online Judge এ। Offline CHT দিয়ে Solve করা যায় এমন কিছু প্রবলেম হল -

• ACQUIRE - Land Acquisition: 1D DP, Relatively Easy.
• APIO10A - Commando: DP Formula Simplify করা একটু কঠিন। বেশ সময় লাগতে পারে।
• CF 660F - Bear and Bowling 4: উপরে অলোচনা করা হয়েছে।
• NKLEAVES - Leaves: উপরে অলোচনা করা হয়েছে।
• CF 631E - Product Sum: 1D DP হলেও একটু কঠিন। Judge Data Strong. Formula বের করতে Time লাগতে পারে।
• CF 319C - Kalila and Dimna in the Logging Industry: Basic Application.

ধন্যবাদ সবাইকে।